Die Lichtgeschwindigkeit

Die Lichtgeschwindigkeit beträgt im Vakuum 2,99792458*10⁸m/s.

Die Messung der Lichtgeschwindigkeit hatte eine große Bedeutung bei der Frage, welche Vorstellung von der Natur des Lichts denn nun die "richtige" sei. Newton und Huygens, aber auch schon andere Physiker vor ihnen, gingen bei ihrer Herleitung des Brechungsgesetzes einmal von einer im dichteren Medium größeren, einmal im dichteren Medium kleineren Lichtgeschwindigkeit aus. Da sie gleichzeitig vehemente Verfechter der Teilchenvorstellung bzw. der Wellenvorstellung des Lichtes waren, sollte eine Messung der Lichtgeschwindigkeit den Zwist entscheiden.

Viel früher beschäftigten sich die Physiker mit der Frage, ob sich Licht mit einer endlichen Geschwindigkeit oder unendlich schnell ausbreitet.
In der Antike ging man meist von einer augenblicklichen Ausbreitung des Lichtes aus. Aber auch in der Neuzeit verfolgte man noch diesen Ansatz. Kepler meinte, dass, da die Lichtausbreitung keine materielle Bewegung darstelle, sie im Medium keinen Widerstand erfahre und sie daher momentan erfolgen müsse.
Auch Descartes nahm an, dass sich das Licht unendlich schnell ausbreite, obwohl er bei seiner Herleitung des Brechungsgesetzes von in dünnem und dichtem Medien unterschiedlicher Lichtgeschwindigkeit ausging. Er begründete seine Annahme so: Würde das Licht vom Mond zur Erde eine endliche Zeit, z.B. eine Stunde, benötigen, würde man eine Mondfinsternis nicht in dem Augenblick sehen, in dem sich Sonne, Erde und Mond auf einer geraden Linie befinden, sondern zwei Stunden später. Dann würde aber der Mond wieder unter einem gewissen Winkel zur Linie Sonne-Erde gesehen. Diesen Winkel konnte man nicht feststellen. Descartes konnte aber nicht ahnen, dass Licht dermaßen schnell ist, dass der tatsächlich vorhandene Winkel zu seiner Zeit nicht gemessen werden konnte.

Galilei versuchte die Frage experimentell zu klären. Zwei Personen, jeder mit einer Lampe, stellten sich gegenüber. Zunächst deckten beide die Lampe mit einer Hand ab. Dann öffnete einer die Abdeckung. Sobald der zweite das Licht sah, öffnete auch er die Abdeckung. Erst wurde das Wechselspiel in geringer Entfernung geübt. Dann vergrößerten die Personen ihren Abstand. Breitet sich das Licht mit endlicher Geschwindigkeit aus, müsste der Abstand zwischen Aufdecken der ersten Lampe und Wahrnehmen der Aufdeckung der zweiten Lampe größer werden. Galilei konnte in seinem Experiment mit einer Entfernung von einer knappen Meile aber keinen Unterschied feststellen. Er folgerte richtig, dass die Lichtgeschwindigkeit, wenn sie nicht unendlich groß sei, doch sehr groß sein müsse.

1676 gelang Ole Christensen Römer der erste Beweis der Endlichkeit der Lichtgeschwindigkeit. Er war seit 1672 Mitarbeiter des Astronomen Giovanni Domenico Cassini. Dieser entdeckte 1675 eine gewisse Unregelmäßigkeit in der Bewegung des innersten Jupitermondes (Io), Die Umlaufzeit war davon abhängig, ob sich die Erde vom Jupiter entfernte oder näherte.

Wenn die Erde sich dem Jupiter nähert, lassen sich die Eintauchungen (A) der Monde in den Schatten beobachten, wenn sie sich entfernt, die Auftauchungen (B).

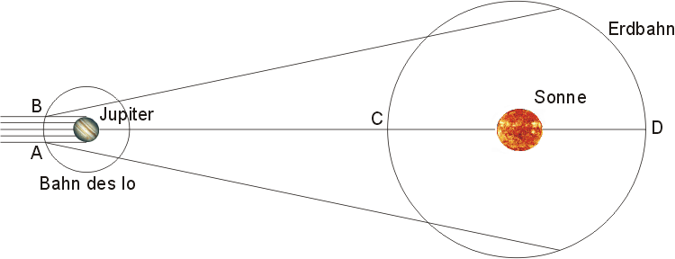
Römer sah, dass sich die Erscheinung bei der Annäherung der Erde beschleunigte und bei ihrer Entfernung verzögerte. Wenn er ferner aus der Umlaufzeit des innersten Mondes, wie sie bei der geringsten Entfernung der Erde vom Jupiter beobachtet wurde (C), die künftigen Verfinsterungen vorausberechnete, so ergab die Wirklichkeit Verspätungen, je weiter sich die Erde vom Jupiter entfernte. Die größte Verspätung maß Römer bei der größten Entfernung der Erde vom Jupiter (D) mit ca. 22 Minuten.
Römer folgerte daraus, dass das Licht ungefähr 22 Minuten brauchte, um den Erdbahndurchmesser zu durchlaufen und damit also die Endlichkeit der Lichtgeschwindigkeit.
Entgegen einiger Veröffentlichungen konnte Römer noch nicht den Wert der Lichtgeschwindigkeit berechnen, da damals der Erdbahndurchmesser noch nicht bekannt war. Mit dem heute bekannten Erdbahndurchmesser von 2,992*10¹¹m ergibt sich aus Römers Beobachtungen eine Lichtgeschwindigkeit von 2,267*10⁸m/s.

Dem Beweis der Endlichkeit der Lichtgeschwindigkeit stimmten zunächst nur wenige Wissenschaftler zu. Erst als auch der englische Astronom James Bradley 1727 aus der Aberration des Lichts auf eine endliche Lichtgeschwindigkeit schloss, erkannte man die Tatsache an.
Das Phänomen der Aberration lässt sich am besten mit einem Fußgänger im Regen vergleichen. Nimmt man an, dass die Regentropfen senkrecht nach unten fallen, so muss man den Regenschirm umso schräger nach vorn halten, je schneller man geht, um nicht vom Regen gertoffen zu werden. Der Regen sei nun das vertikal von einem Fixstern einfallende Licht, der Schirm das Fernrohr, mit dem der Stern beobachtet wird. Da sich die Erde bewegt (sowohl um die Sonne, als auch um sich selbst), muss das Fernrohr schräg gehalten werden.

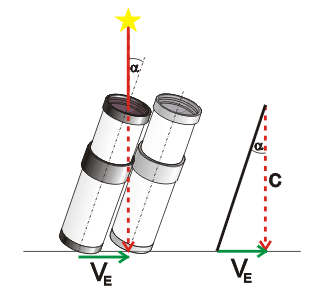
Es ergibt sich , und damit .
Für einen Beobachter auf der Erde beschreibt der Fixstern eine Ellipse. Genaue Messungen haben für den Umlauf der Erde um die Sonne α = 20,48" ergeben, für die Drehung der Erde um sich selbst α = 0,32". Letzteres kann man vernachlässigen.
Bei einer Umlaufgeschwindigkeit der Erde um die Sonne von v_E=2,977*10⁴m/s bekommt man für die Lichtgeschwindigkeit c = 2,998*10⁸m/s.

Die bisher dargestellten Methoden benutzten die Weite des Weltraums zur Bestimmung der Lichtgeschwindigkeit. Nun bemühte man sich die Lichtgeschwindigkeit auch auf der Erde zu messen, um dann auch Messungen in verschiedenen Medien zu ermöglichen. Das Problem war, wegen der geringen Distanzen äußerst kurze Zeiten zu messen, denn die enorme Größe der Lichtgeschwindigkeit war ja nun bekannt.

Als erster löste Hippolyte Fizeau 1849 das Problem der Kurzzeitmessung. Er ließ das Licht durch ein rotierendes Zahnrad laufen, nach einer großen Wegstrecke (8,633 km) reflektieren und noch einmal durch das Zahnrad laufen (Lichtquelle und Zahnrad plazierte er übrigens auf einen Hügel vor seinem Haus in Paris und den Spiegel auf den Montmatre).

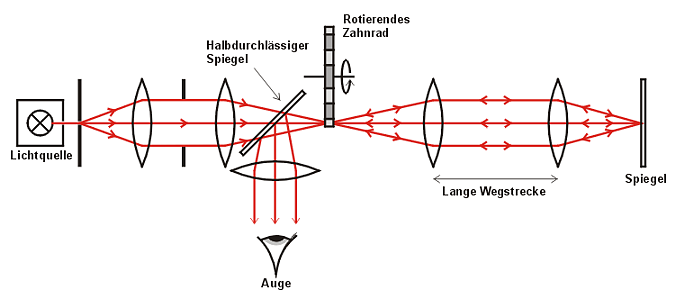
Bei stillstehendem Zahnrad traf das reflektierte Licht wieder dieselbe Zahnlücke. Beschleunigte man die Drehung des Zahnrades, wurde immer mehr Licht vom nachfolgenden Zahn abgedeckt, bis bei einer bestimmten Rotationsgeschwindigkeit kein Licht mehr im Auge ankam.
Bei stärkster Abdunklung für den Beobachter war das Rad etwa von Zahnlückenmitte zur nächstfolgenden Zahnmitte vorgerückt. Bei insgesamt 720 Zähnen hatte sich das Rad dann um den 1440sten Teil einer vollen Drehung weiterbewegt. Bei einer Drehfrequenz f_Z = 12,6 Hz entsprach das der Zeit t = 1/(f_Z*1440) = 5,5*10^-5s und für einen Weg von s = 2*8,633 km ergab das c = s/t = 3,13*10⁸m/s.
Die Genauigkeit der Messung wurde noch von der Breite der Zähne und der Fähigkeit des Beobachters, die maximale Dunkelheit wahrzunehmen, begrenzt.

1850 verbesserte Foucault den Versuchsaufbau, indem er anstelle des Zahnrades einen Drehspiegel verwendete.

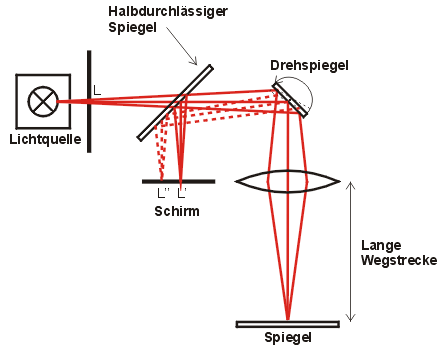
Das Licht fällt auf einen Drehspiegel und von dort nach Durchlaufen einer gewissen Wegstrecke auf einen Umlenkspiegel. Die fokussierende Linse ist eine Verbesserung von Michelson - Foucault benutzte zur Fokussierung einen Hohlspiegel. Bekannt ist auch, dass Michelson seine Versuche zwischen zwei Bergspitzen in Kalifornien durchführte, deren Entfernung von 35,4km bis auf 5cm genau vermessen war.
Das reflektierte Licht trifft wieder auf den Drehspiegel, der sich aber inzwischen um den Winkel α weitergedreht hat. So entsteht auf dem Schirm ein Bild L'' der Lichtquelle L statt eines Bildes L' bei ruhendem Spiegel. Je schneller sich der Spiegel dreht, desto größer ist der Abstand a zwischen L' und L'' (Die Winkelabweichung beträgt 2*α).
Näherungsweise kann man a als Kreisbogen eines Kreises mit dem Radius r = Abstand zwischen Lichtquelle und Drehspiegel sehen. Dann gilt , also .
Das Licht durchläuft den Weg s = 2 * Abstand zwischen Drehspiegel und Umkehrspiegel. Die Zeit, die es dafür benötigt, bekommt man mit der Drehzeit T des Drehspiegels, bzw. seiner Frequenz f_D: und .
Die Lichtgeschwindigkeit beträgt dann .
Mit den ungefähren Werten von Michelson s=70,8km, f_D=530Hz, r=2m und a=3,146m (die letzten beiden Werte sind geschätzt, da mir unbekannt) ergibt sich für die Lichtgeschwindigkeit c=299771km/s. Michelson selbst erhielt c=299797km/s.

Da Foucault nur einen Lichtweg von 20m benutzte, konnte er mit seinem Versuchsaufbau auch die Lichtgeschwindigkeit in einem optisch dichteren Medium (Wasser) messen. Sie stellte sich als kleiner heraus, was der Teilchentheorie des Lichts den Todesstoß versetzte.

Heutzutage bestimmt man die Lichtgeschwindigkeit mit elektronischer Pulsung oder Modulation des Lichts, oder durch Messung der Laufzeiten von Satellitensignalen, da man inzwischen wieß, dass sich jedes elektromagnetische Signal mit Lichtgeschwindigkeit ausbreitet.

Ich habe die Lichtgeschwindigkeit mit dem Modulationsverfahren in Luft und in Wasser gemessen.

Als Lichtquelle dient eine Leuchtdiode. Sie wird mit Wechselstrom der Frequenz 50,1 MHz betrieben. Deshalb sendet sie Licht mit schnell aufeinander folgenden Helligkeitsschwankungen aus. Nach dem Durchlaufen eines bestimmten Lichtweges wird in einer Photodiode eine Wechselspannung hervorgerufen. Die beiden Wechselspannungen werden mit dem Oszilloskop verglichen.

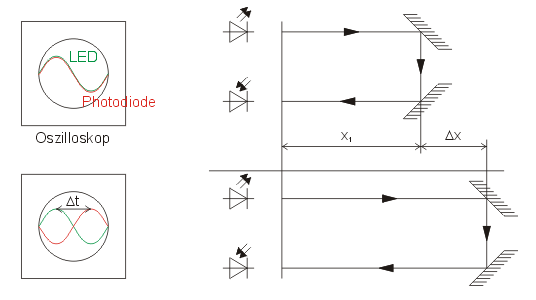
Nach Durchlaufen des Lichtweges l₁=2*x₁ sei die Phasendifferenz der beiden Wechselspannungen null. Nun wird der Lichtweg so vergrößert, bis sie eine Phasendifferenz haben.
Das bedeutet, dass das Lichtsignal um die Zeitdauer einer halben Periodendauer der Wechselspannung später bei der Photodiode ankommt, d.h. .
Für die Lichtgeschwindigkeit gilt also: .

Ich habe Δx=1,485m gemessen und damit für die Lichtgeschwindigkeit c=2,976*10⁸m/s erhalten.

Zur Messung der Lichtgeschwindigkeit in Wasser wird eine mit Wasser gefüllte Küvette in den Strahlengang vor die Photodiode gestellt.

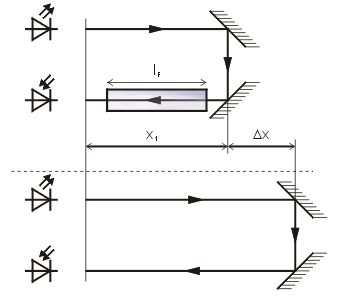
Nach Durchlaufen des Lichtweges l₁=l_F+(2*x₁-l_F) sei die Phasendifferenz der beiden Wechselspannungen null.
Die Küvette wird wieder entfernt. Nun wird der Lichtweg solange verlängert, bis die Phasendifferenz wieder null ist, d.h. das Licht die gleiche Zeit braucht wie vorher, um von der Leuchtdiode zur Photodiode zu gelangen.
Der Lichtweg ist nun l₂=2*x₁+2*Δx.
Es gilt: also und .
Gleichsetzen und Auflösen nach c_Wasser liefert .
Ich habe Δx=0,19m und l_F=1,00m gemessen. Damit beträgt die Lichtgeschwindigkeit in Wasser c_Wasser=2,157*10⁸m/s (wirklicher Wert: 2,24*10⁸m/s).